Zu diesem Fall sind alternative bzw. kontroverse Interpretationen vorhanden:
- Krummheuer/Brandt: Die Lehrerin hilft Efrem (1)
- Komparation der Fälle ‚Wayne hilft Efrem (1/2)‘ und ‚Die Lehrerin hilft Efrem (1/2)‘
Fälle aus demselben Erhebungskontext:
Falldarstellung
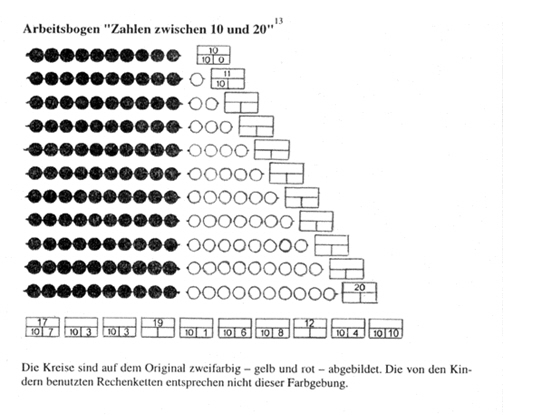
In den ausgewählten Szenen wird jeweils der Arbeitsbogen „Zahlen 11 bis 20“ bearbeitet (siehe Abbildung). Zum leichteren Textverständnis werden die dort abgebildeten Kreise in den Analysen als „Darstellungsebene der Kreise“, „Kreisdarstellung“ oder kurz „Kreisebene“ bezeichnet. Die Lösungskästchen der Aufgaben werden einzeln mit „oben“ bzw. (unten) „links“ und (unten) „rechts“ angesprochen, wobei entsprechend der Aufgabenstellung die rechten Kästchen Einerkästchen bzw. Einerspalte genannt werden. Alle drei Kästchen einer Aufgabe werden sprachlich als „Block“ zusammengefasst („Blockdarstellung“, „Blockebene“).
Es werden Paarinteraktionen diskutiert, bei denen jeweils ein Helfender zu Efrem an den Tisch kommt. Zunächst erhält Efrem Hilfe von Wayne für den oberen Teil des Arbeitsblattes [Fälle Wayne hilft Efrem (1) und (2)], danach wendet sich Efrem an die Lehrerin, die zwei Aufgaben des zweiten Teiles mit ihm bearbeitet [Fälle Die Lehrerin hilft Efrem (1) und (2)].
Efrem bearbeitet weiter das Arbeitsblatt „Zahlen 11 bis 20“. Er hat den oberen Teil bearbeitet, nachdem Wayne es ihm beigebracht hat <464>. Er beendet diesen Teil des Arbeitsbogens und ruft die Lehrerin <506,513>, die ihm gegenüber mit Marina arbeitet. Er wendet seinen Blick der unteren Aufgabenreihe zu puh . jetzt kommt eine s c h w e r e Aufgabe < 517> und ruft dann erneut die Lehrerin <522>. Diese beendet schließlich ihre Erklärungen für Marina und kommt auf Efrem zu:
| 529 | Efrem | zeigt flüchtig auf den unteren Aufgabenteil ich weiß nich was da hin kommt |
| 530 | L | zeigt den 1. Block in der unteren Aufgabenreihe kuck mal , was steht da . siebzehn ist gleich / |
| 530.1 | < L | zeigt auf ein Kästchen zeigt ein anderes Kästchen |
| 531 | <Efrem | zehn / (sieben) |
| 532 | L | so . greift nach Efrems Rechenkette jetzt mach mal hier ne Zehn / |
| 533 | zeigt auf die Perlen der Kette jetzt steht hier zehn / und drei | |
| 534 | Efrem | mmh / |
| 535 | L | leg mir das mal hin zeig mir das mal . ne Zehn / und ne Drei |
| 536-537 | Efrem | bewegt zehn Perlen an seiner Kette zehn und eine Drei . zehn /. tut drei helle Perlen dazu |
| 538 | L | mmh / wieviel haste dann / |
| 539 | Efrem | zählt die Perlen leise einzeln ab… dreizehn |
| 540 | L | mmh / und wo schreibst du die hin / Julian kommt auf den Tisch zu |
| 541 | < Efrem | hier . schreibt |
| 542 | < L | mmh / dann machs |
Interpretation
Die beiden in der Interaktionsanalyse beschriebenen Ansätze lassen sich als zwei Argumentationsstränge zur Aufgabe ausmachen:
- Bilden einer additiven Zerlegung am Beispiel der Musteraufgaben und
- Heranziehen der Rechenkette.
Efrem hat auf die gesamte untere Reihe gezeigt und damit eventuell angedeutet, dass er den „Typ“ dieser Aufgaben nicht versteht. Geht man davon aus, dass das Ziel die Erklärung des Aufgabentyps ist, lassen sich die Argumentationen wie folgt wiedergeben:
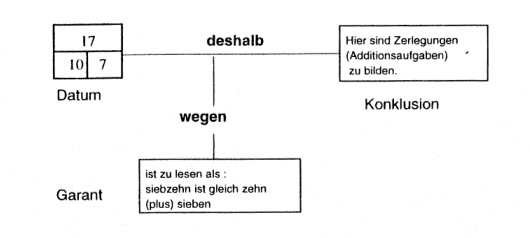
Argumentation anhand der Beispielaufgabe <526-531>
Der ausgefüllte Block wird von der Lehrerin durch kuck mal als Datum präsentiert. Die mit Efrem gemeinsam daraus erlesene Additionsaufgabe dient als Garant und lässt auf den Arbeitsauftrag schließen: Hier sind Additionsaufgaben zu bilden, was als Konklusion jedoch ungenannt bleibt.
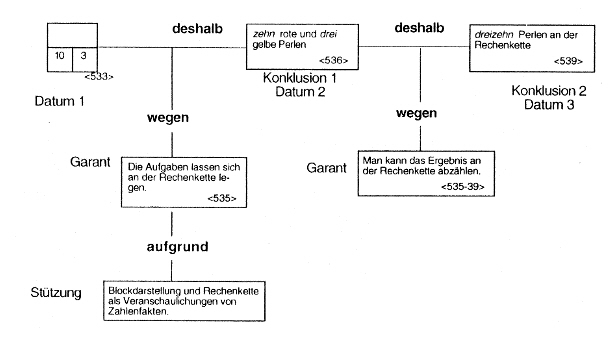
Argumentation mit Hilfe der Rechenkette <531-542>
Die Lehrerin greift auf die Rechenkette als Argumentationshilfe zurück. Die Zehn und die Drei aus dem vorliegenden Block werden zu Daten, die man an der Rechenkette legen kann. Damit wird ein Zusammenhang zwischen Rechenkette und Rechenblock „hergestellt“: Die Zahlen in den Kästchen sind als Anzahlen für Perlen zu deuten (Konklusion 1). Die mit wieviel haste dann <538> angesprochene Additionsaufgabe ist so auf die Rechenkette zu übertragen und dort zu lösen, was die Lehrerin Efrem überlässt. Dieser ermittelt das Ergebnis zählend (Konklusion 2).
Im nächsten Schritt werden die dreizehn Perlen der Rechenkette wieder auf den Arbeitsbogen übertragen. Mit der Frage und wo schreibst du die hin/ schafft die Lehrerin erneut explizit einen Zusammenhang zwischen den Blöcken auf dem Arbeitsbogen und der Rechenkette, bleibt jedoch auf der Performanzebene: Das an der Rechenkette ermittelte Ergebnis ist auf dem Arbeitsbogen einzutragen (Garant).
Hier wird nur der Ort thematisiert, an dem das an der Rechenkette ermittelte Ergebnis einzutragen ist. Der Zusammenhang zwischen den Darstellungen als unterschiedliche Repräsentationen der Zerlegung der Zahlen im Dezimalsystem wird somit auf der Handlungsebene hervorgebracht. Efrem weist auf das richtige Kästchen und trägt die Dreizehn ein (Konklusion 3). Hier kann er an einen fundamentalen Erfahrungswert aus dem Mathematikunterricht anknüpfen, der durch die Bestätigung der Lehrerin erneut bekräftigt wird: In leere Kästchen sind die Ergebnisse von Rechenaufgaben einzutragen.
Der Zusammenhang zwischen beiden Aufgaben wird nicht expliziert. Vielmehr dokumentiert sich im gesamten Interaktionsprozess ein narratives Erklärungsmuster (Krummheuer 1997a). Dieses zeichnet sich gerade dadurch aus, dass die unterstellte Rationalität der Handlungsabfolge nicht thematisiert wird.
Partizipationstheoretische Überlegungen zur Funktion der Sprechenden
Auch hier werden die beiden rekonstruierten Argumentationsstränge betrachtet.
Block als Additionsaufgabe lesen
Die Lehrerin verweist mit kuck mal, was steht da <530> ausdrücklich auf das Arbeitsblatt und entzieht sich damit Teilen der Verantwortung. Die Formulierung ist gleich , die die Idee einer Gleichung beinhaltet, ist jedoch nicht unmittelbar dem Arbeitsblatt zu entnehmen – auch wenn die Lehrerin dies mit kuck mal durchaus ausdrücken könnte. Sie ist hier für die Idee der Addition verantwortlich, das Arbeitsblatt liefert die Zahlen. Efrem liest die Zahlen fragend aus den Kästchen vor und antwortet somit „auf Probe“ (vgl. Interpretation zu den Zeilen <445> und <448> in den Szenen ‚Wayne hilft Efrem (1/2)‘). Dabei ist er an der Hervorbringung der Additionsaufgabe als „Sprachrohr“ beteiligt (Imitierer): Die Lehrerin zeigt ihm die Zahlen und bestätigt mit so abschließend, dass diese so in das Argumentationsformat (Additionsaufgabe) einzubringen sind.
| Block als Additionsaufgabe | ||
| WORTWAHL Arbeitsblatt |
1. Block der Aufgabenreihe (Vorgabe der Zahlen) | Formulator |
| Lehrerin: <530> <530.1-532> |
siebzehn ist gleich / zeigt jeweils auf die entsprechenden Kästchen so |
Traduzierer |
| Efrem: <531> |
zehn / (sieben) | Imitierer |
Rückgriff auf die Rechenkette
Die Lehrerin „verlässt“ sich weiter auf die Sinnhaftigkeit der auf dem Arbeitsblatt eingesetzten Aufgaben – gibt also Verantwortung ab. Mit jetzt steht hier zehn / und drei verweist sie explizit auf die Zahlen auf dem Arbeitsblatt. Diese Äußerung wurde als Selbstkorrektur der vorgegriffenen Anweisung jetzt mach mal hier ne Zehn interpretiert. Somit manifestiert sich hier auch die Verantwortlichkeit für die erste Äußerung. Die Idee, die Aufgabe an der Rechenkette zu legen, wird von der Lehrerin nochmals geschärft rephrasiert. Efrem führt die an ihn herangetragene Handlung aus und „rezitiert“ die Lehrerin fast wörtlich.
| Übertragen auf die Rechenkette | ||
| WORTWAHL Arbeitsblatt |
2. Block der Aufgabenreihe | Formulator |
| Lehrerin <532> <535> |
jetzt mach mal hier ne Zehn leg mir das mal hin zeig mir das mal ne Zehn / und ne Drei |
Traduzierer |
| Efrem: <536> |
bewegt zehn Perlen an seiner Kette zehn und eine Drei . zehn /. tut drei gelbe Perlen dazu | Imitierer |
Das Ergebnis kann nun an der Rechenkette ermittelt werden. Dass dazu die Anzahl der Perlen abgezählt werden muss, wird durch die Frage der Lehrerin deutlich. Efrem ist „ausführend“ tätig, formuliert schließlich die Lösung. Durch den Arbeitsauftrag Hinschreiben drückt die Lehrerin aus, dass dieses Ergebnis wieder auf den Arbeitsbogen zu übertragen ist. Mit hier bestimmt Efrem lediglich auf der Ebene des Arbeitsbogens die richtige Stelle und wird erst ausführend tätig, nachdem die Lehrerin dies bestätigt hat. Der Zusammenhang zwischen der Rechenkette und dem Arbeitsblatt, der als Motiv dieser Abfolge von Äußerungen gesehen werden kann, bleibt somit gänzlich in der Verantwortung der Lehrerin.
| Ausrechnen an der Rechenkette | ||
| Lehrerin <538> |
wieviel haste dann/ | Kreator |
| Efrem <539> |
zählt die Perlen leise einzeln ab … dreizehn | Paraphrasierer |
| Ergebnis auf den Arbeitsbogen übertragen | ||
| Lehrerin <540> <542> |
und wo schreibst du die hin / mmh / dann machs |
Kreator |
| Efrem <541> |
hier . schreibt | Paraphrasierer |
Transkriptionszeichen
Name: namentlich identifizierter Schüler
S; S1; S2: namentlich nicht identifizierte Schüler
Ss: mehrere Schüler
L: Lehrerin
/ bzw. \ : Stimme wird gehoben bzw. gesenkt
– Stimme bleibt in der Schwebe
. .. … Sprechpausen (mehr Punkte entsprechen längeren Pausen; Transkript enthält in den Sprechpassagen keine Satzzeichen.)
<: sprechen teilweise gleichzeitig
g e s p e r r t: gedehnt/langsam gesprochen
kursiv : Ausdruck, Gestik, Mimik, Handlungen etc.
fett : betont gesprochene Wörter
+: Ende des angegebenen Ausdrucks, Gestik, Mimik, Handlung, Atemholen
(Wort): eingeklammerte Wörter sind nicht zweifelsfrei verständlich
(unverständlich): gänzlich unverständliche Äußerung des fokussierten Schülers
Literatur
Maier, H./Voigt, J. (1989): Die entwickelnde Lehrerfrage im Mathematikunterricht, Teil 1 und 2. In: mathematica didactica 12: 23-55; 87-94
Nutzungsbedingungen:
Das vorliegende Dokument ist ausschließlich für den persönlichen, bzw. nicht-kommerziellen Gebrauch bestimmt – es darf nicht für öffentliche und/oder kommerzielle Zwecke außerhalb der Lehre vervielfältigt, bzw. vertrieben oder aufgeführt werden. Kopien dieses Dokuments müssen immer mit allen Urheberrechtshinweisen und Quellenangaben versehen bleiben. Mit der Nutzung des Dokuments werden keine Eigentumsrechte übertragen. Mit der Verwendung dieses Dokuments erkennen Sie die Nutzungsbedingungen an.