Zu diesem Fall sind alternative bzw. kontroverse Interpretationen vorhanden:
- Krummheuer/Brandt: Wayne hilft Efrem (1)
- Komparation der Fälle ‚Wayne hilft Efrem (1/2)‘ und ‚Die Lehrerin hilft Efrem (1/2)‘
Fälle aus demselben Erhebungskontext:
Falldarstellung
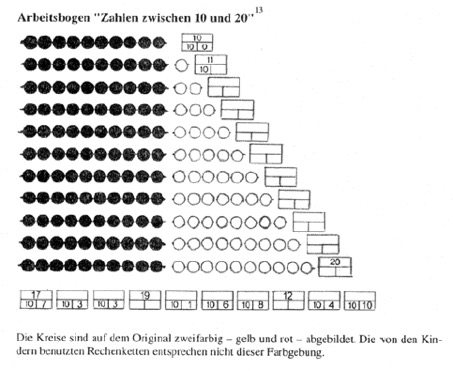
In den ausgewählten Szenen wird jeweils der Arbeitsbogen „Zahlen 11 bis 20“ bearbeitet (siehe Abbildung). Zum leichteren Textverständnis werden die dort abgebildeten Kreise in den Analysen als „Darstellungsebene der Kreise“, „Kreisdarstellung“ oder kurz „Kreisebene“ bezeichnet. Die Lösungskästchen der Aufgaben werden einzeln mit „oben“ bzw. (unten) „links“ und (unten) „rechts“ angesprochen, wobei entsprechend der Aufgabenstellung die rechten Kästchen Einerkästchen bzw. Einerspalte genannt werden. Alle drei Kästchen einer Aufgabe werden sprachlich als „Block“ zusammengefasst („Blockdarstellung“, „Blockebene“).
Es werden Paarinteraktionen diskutiert, bei denen jeweils ein Helfender zu Efrem an den Tisch kommt. Zunächst erhält Efrem Hilfe von Wayne für den oberen Teil des Arbeitsblattes [Fälle Wayne hilft Efrem (1) und (2)], danach wendet sich Efrem an die Lehrerin, die zwei Aufgaben des zweiten Teiles mit ihm bearbeitet [Fälle Die Lehrerin hilft Efrem (1) und (2)].
Wayne wird von der Lehrerin mit dem Auftrag, den Kindern zu zeigen, wie man das macht . ja / wie man das rauskriegt was man reinschreiben muss <402-403> als Helfer ausgeschickt. Damit scheint sie alleiniges Abschreiben bzw. Vorsagen als Hilfe auszuschließen. Wayne nimmt seinen Arbeitsbogen und wendet sich zuerst Efrem zu:
| 429-431 | Wayne | kommt mit seinem Aufgabenblatt und stellt sich neben Efrem, der sich über sein Erscheinen freut hier sind doch zehn \ zeigt auf die Kästchen auf Efrems Blatt und hier eins . da musst du doch /. kuck doch \ (unverständlich) |
| 432 | Efrem | ja \ eine Eins \ ja |
| 433 | Wayne | ja + da müsste ne Eins (jetzt rein) (unverständlich) |
| 434-434.1 | Efrem | und jetzt zeigt immer die gelben Kreisreihen von links nach rechts entlang zwei, drei, vier, fünf |
| 435 | Wayne | zeigt auf die Kästchen guck jetzt / |
| 436 | <Efrem | sechs, sieben, acht |
| 437 | <Wayne | (unverständlich) |
| 438 | Efrem | neun, zehn . bis hier sollen wir (eins) hinschreiben + \ stimmts / |
| 439-439.1 | Wayne | zeigt auf das Kästchen guck mal und hier musst du jetzt erst mal hier ne Eins machen |
| 440 | Efrem | holt einen Stift aus der Mappe, schreibt eins / |
| 441 | Wayne | zeigt auf das Kästchen hier musst du jetzt ganz oben eine Zwölf machen / |
| 442 | Efrem | du meinst wieder s (unverständlich) |
| 443- 444 | Wayne | nein \ ne Zwölf \ .. gut / zeigt auf die Kästchen und dann hier / . schaut auf das Ergebnis auf seinem eigenen Arbeitsbogen |
| 445 | Efrem | eine Zehn / schreibt es hin |
| 446 | Wayne | schaut nochmal kurz auf sein Blatt jaha / zehn \ .. und dann musst du – |
| 447 | <Wayne | (unverständlich) wendet sich zu Carola (unverständlich)+ |
| 447.1 | <Carola | wendet den Kopf zu Wayne (unverständlich) |
| 448 | Efrem | und eine Zwei / |
| 450 | <Wayne | nickt mit dem Kopf mmh / kannst du das jetzt / |
| 451 | < Efrem | schreibt ä m \ |
| 452- 453 | Wayne | kuck mal \ hier ist doch die Kästchen zeigend zwölf dreizehn vier zehn fünfzehn sechzehn siebzehn + und hier / in diese Kästchen immer zehnsf (unverständlich) |
| 453 | < Efrem | und diese Kästchen immer auch drei vier fünf sechs |
| 455 | <Wayne | ja \ ja \ klopft mit seinem Stift auf den Tisch so \ |
| 456 | Efrem arbeitet alleine weiter. | |
Interpretation
In der Helferszene Wayne und Efrem ließen sich zunächst zwei unterschiedliche Herangehensweisen rekonstruieren, die dann in eine gemeinsame dritte Argumentation einfließen:
- Wayne möchte den Arbeitsbogen zeilenweise bearbeiten und hält sich beim Ausfüllen der Kästchen streng an die Schreibrichtung.
- Efrem greift eine Eins auf und bringt die abgebildeten gelben Kreise mit der Einerspalte in Verbindung.
- Wayne und Efrem geben vertikal die Zahlen für die Kästchen an und beziehen sich dabei nur auf die Blockdarstellung.
Argumentation in der zeilenweisen Bearbeitung <429-451>
Hier wird der Argumentationsstrang betrachtet, der durch die Äußerungen <429-431;433;435;439;443;446 und 450> (Wayne) sowie die Äußerungen <432,442,445,448 und 451 > (Efrem) gebildet wird:
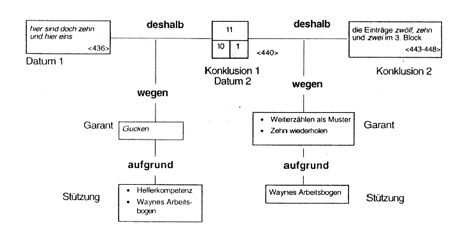
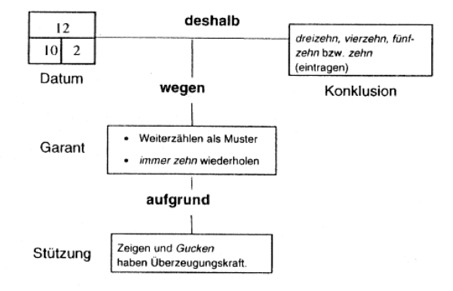
Mit doch versucht Wayne, das Datum hier sind doch zehn und hier eins <430-431> als gemeinsame Gesprächsgrundlage zu etablieren. Dabei wurde in der Interaktionsanalyse davon ausgegangen, dass es sich bei der Zehn um die im zweiten Block schon eingetragene Zehn handelt. Die Eins scheint auch ‘irgendwo’ auf dein Arbeitsblatt als Ziffer vorhanden, jedoch konnte nicht endgültig geklärt werden, welche Eins hier gemeint ist. Durch Gucken lässt sich jedoch erschließen, dass die Eins in das rechte untere Kästchen einzutragen ist <433-W,439-W,440-E>. Mit der schriftlichen Fixierung der Eins akzeptiert Efrem sowohl die Schlussmöglichkeit, die nur durch kuck doch angesprochen wird, als auch das Ergebnis, das nun als Datum 2 weiter in die Argumentation eingehen kann. Die weitere Schlussfolgerung basiert auf dem nun ausgefüllten Block der zweiten Reihe. Mit zwölf <441,443> rekurriert Wayne zunächst auf die aufsteigende Zahlenfolge der Gesamtanzahl. Auch Efrem vermutet eine Regelmäßigkeit daraus entnehmen zu können <442> -jedoch können sie sich nicht darüber verständigen.
Bei der Hervorbringung der Konklusion sind beide beteiligt: zwölf <441;443> wird von Wayne genannt und Efrem ergänzt eine Zehn <445> sowie und eine Zwei <448>.
Efrem fixiert schrittweise die Ergebnisse auf seinem Arbeitsbogen. Die jeweils eingeschobenen Bestätigungen durch Wayne <446;450> machen Efrems Aussagen zu akzeptierten Schlussfolgerungen. Wayne schaut dabei wiederholt auf seinen Arbeitsbogen, der somit auch als Stütze herangezogen wird.
Auffällig erscheint hier, dass Wayne darauf beharrt, die Kästchen zeilenweise in Schreibrichtung auszufüllen. Da er dabei jedoch nicht auf die dargestellten Kreise bzw. die Zerlegung der Zahlen eingeht, kann er für die einzutragenden Zahlen so allein die Systematik der Blockdarstellung heranziehen, die erst durch die vertikale Betrachtung erschlossen werden kann. Waynes zu weiten Teilen schon ausgefüllter Arbeitsbogen wird durch diese widersprüchlich erscheinende Darbietung der Erklärung in seiner Funktion als Stützung hervorgehoben.
Argumentation bei der Betrachtung der gelben Kreise <432-438>
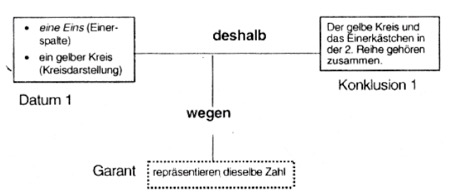
Wahrscheinlich stimmt Efrem schon in <432> zu, dass in dem Kästchen der Einerspalte in der zweiten Reihe eine Eins zu stehen hat. Danach geht er aber dazu über, die Anzahl der abgebildeten gelben Kreise aller Reihen zu bestimmen. Er bringt hier einen Zusammenhang zwischen dem gelben Kreis der zweiten Reihe und dem rechten unteren Kästchen im zweiten Block hervor.
Efrem zählt die gelben Kreise nicht einzeln ab, sondern deutet lediglich durch seine Handbewegung einen Zählprozess an. Die ‘Zeigbarkeit’ der Kreise ermöglicht zugleich die Abzählbarkeit der Kreise. Die Kreise werden somit von Efrem als Repräsentanten von (An)zahlen gesehen. Die Zunahme um jeweils einen Kreis erkennt er entweder optisch (Abbildung als Garant) oder er geht auf Erklärungen der Lehrerin zum Arbeitsbogen zurück. Die so bestimmten Anzahlen bringt er in einem nächsten Schritt mit den Einerkästchen zusammen, in die nun etwas eingetragen werden kann. Er geht also von einer Systematik des Arbeitsblattes aus.
Argumentation beim vertikalen Ausfüllen der Kästchen <452-456>
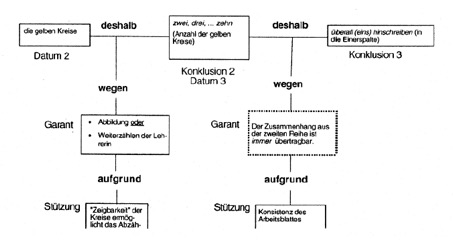
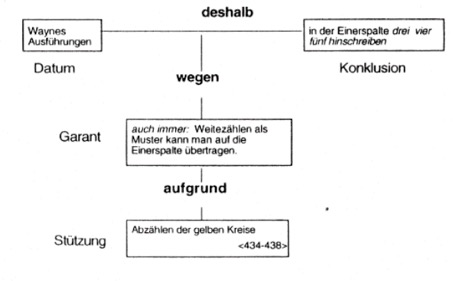
Der gemeinsam ausgefüllte Block der dritten Reihe wird nun Grundlage für eine weitere kollektive Argumentation. Die dort eingetragenen Zahlen gehen als Datum in die Argumentation ein. Durch das Zeigen auf die einzelnen Kästchen der Blöcke wird die Gleichartigkeit der Blöcke hervorgehoben. Das Zeigen auf bestimmte Kästchen rekurriert dabei auf die Überzeugungskraft von Gucken: An den gezeigten Stellen kann eine Bearbeitungsmöglichkeit des Arbeitsbogens erblickt (erkannt) werden.
Durch Weiterzählen können so aus der Zwölf die Zahlen für die anderen oberen Kästchen bestimmt werden. Die Wiederholung der Zehn wird durch immer ausgedrückt. Durch und scheint Efrem Waynes Ausführungen zu akzeptieren und damit wird hier nochmals Waynes Kompetenz unterstrichen. Einerseits rekurriert Efrem also direkt auf Waynes Ausführungen: das Weiterzählen als Muster lässt sich auf die Einerspalte übertragen. Andererseits ergreift Efrem hier bei der Einerspalte das Wort – und knüpft somit auch an die eigenen Ausführungen an:
Die Anzahl der gelben Kreise hatte er in <434-438> ermittelt und mit der Einerspalte in Verbindung gebracht. Dies vermittelt ihm hier eventuell eine gewisse Sicherheit, Waynes schematischer Ausfülltechnik zu folgen.
Partizipationstheoretische Überlegungen zur Funktion der Sprechenden
Für die drei Argumentationsstränge soll nun im Folgenden die Funktionen der Beteiligten für die Beiträge analysiert werden.
Zeilenweise Bearbeitung
Waynes Bemühungen wurden dahingehend interpretiert, dass er Efrem die Lösungen nicht nur ‘vorsagen’ möchte, sondern durch das zeilenweise Ausfüllen auch einen Erkenntnisgewinn bei Efrem erhofft. Dieser erklärende Gehalt, der nach unserer Analyse der zeilenweisen Bearbeitung zugeschrieben wird, soll hier als Motiv partizipationstheoretisch beleuchtet werden. Wayne ‘wählt’ dabei die Reihenfolge der Kästchen (zeilenweise). Die Zahlen der von Wayne gewählten Kästchen werden durch das Arbeitsblatt vorgegeben, das ‘Motiv’, durch seine Lösungsweise das Arbeitsblatt ‘erklären’ zu wollen, bleibt bei Wayne.
Efrem folgt ab <440> der von Wayne vorgegebenen Arbeitsrichtung und trägt die Eins und die Zwölf ein. Er akzeptiert damit auch Waynes Kompetenz als Helfer. Dies ermöglicht Efrem eine ‘Antwort auf Probe’ <445>, die er ‘fragend’ hervorbringt. Wayne übernimmt durch die nachfolgende Bestätigung die Verantwortung für diese Lösung. Dieses Vorgehen wiederholt sich für die Zwei im entsprechenden Einerkästchen:
| Vorgabe der Arbeitsrichtung | |||
| Wayne: <439> <441> <443> <446> |
guck mal und hier musst du jetzt erst mal zeigt auf das Kästchen hier musst du jetzt ganz oben zeigt auf das Kästchen und dann hier und dann musst du – |
Kreator | |
| Ausfüllen der Kästchen | |||
| WORTWAHL Arbeitsblatt | Zahlen bzw. Lösungen der entsprechende Kästchen | Formulator | |
| Wayne: <430f> <433> <439> <441> |
hier eins ne Eins… hier ne Eins machen hier eine Zwölf machen |
Traduzierer | |
| Efrem: <440> |
schreibt eins/ | Imitierer | |
| Efrem: <445> <448>;<451> |
eine Zehn schreibt und eine Zwei; schreibt |
Imitierer | |
| Wayne: <446> <450> |
jaha / zehn nickt mit dem Kopf mmh / |
Traduzierer | |
Betrachtung der gelben Kreise
Efrem greift zunächst Waynes Worte auf und scheint sich ihm als Imitierer anzuschließen <430-431>. Es zeigt sich aber, dass Efrem durch die Zuordnung Zahlwortreihe – gelbe Kreise eigene Überlegungen anknüpft und somit die Eins als Traduzierer aufgreift. Das vertikale Abzählen der Kreise kann somit als Motiv herausgegriffen werden, das von Efrem in die Interaktion eingebracht wird:
| Zuordnung Eins – gelber Kreis | ||
| WORTWAHL Wayne <430> |
und hier eins | Formulator |
| Efrem: <432> |
ja \ eine Eins \ ja | Traduzierer |
| vertikale Betrachtung | ||
| WORTWAHL Arbeitsblatt |
die abgebildeten Kreise (Anzahlen) | Formulator |
| Efrem: <434-438> |
und jetzt (…) zwei, drei, vier (…) zehn | Traduzierer |
Vertikales Ausfüllen der Kästchen
Wayne übernimmt nun die vertikale Bearbeitungsrichtung von Efrem, knüpft dabei jedoch nicht an die Kreisdarstellung an. Durch die Beschränkung auf die Blockebene kommt der Abfolge der Lösungen erneut ein Erkenntnis bringender Gehalt zu (kuck mal). In der Übernahme der vertikalen Betrachtung und die Beschränkung auf die einzutragenden Zahlen erscheint Wayne zunächst als Imitierer, da auch die Wortwahl durch den Arbeitsbogen vorgegeben ist. Andererseits hat er (als Erstklässler) wohl kaum eine Möglichkeit, diese Übernahme der vertikalen Betrachtung auf die Blockdarstellung sprachlich auszudrücken, ohne auf die Zahlwortreihe – und damit auf Lösungen der einzelnen Kästchen – zurückzugreifen. Somit wird ihm hier als (Paraphrasierer) eingeschränkt die Wortwahl zugeschrieben.
Efrem wiederholt die von ihm schon im Zusammenhang mit den gelben Kreisen hervorgebrachte Zahlwortreihe, betrachtet nun aber ebenfalls die auszufüllenden Kästchen. Schon in <438> möchte Efrem die Anzahlen der gelben Kreise hinschreiben. Auch wenn nicht eindeutig rekonstruierbar welches Kästchen er dafür vorgesehen hat, lässt sich hier sein Bemühen erkennen, die beiden vom Arbeitsbogen angebotenen Darstellungen für die dezimale Zerlegung miteinander zu verbinden. Gelingt ihm in <454> als Imitierer der Rückgriff auf seine in <434-438> ausgedrückte Idee, so kann er die Darstellung der Kreise in der Interaktion ‘einsichtsvoll’ nutzen.
| vertikale Betrachtung | ||
| MOTIV Efrem <434-438> |
und jetzt (…) zwei, drei, vier (…) zehn | Initiator |
| WORTWAHL Arbeitsblatt |
Lösungen der Kästchen | (Formulator) |
| Wayne: <452-453> |
kuck mal \ hier ist doch die Kästchen zeigend zwölf, dreizehn (…) , siebzehn+ und hier / in diese Kästchen immer zehnsf | (Paraphrasierer) |
| Efrem: <454> |
und in diese Kästchen immer auch drei vier fünf sechs | Imitierer |
Eine zusammenfassende Betrachtung der Argumentationsanalyse und der Partizipationsanalyse erfolgt in Verbindung mit der Komparation.
Transkriptionszeichen
Name: namentlich identifizierter Schüler
S; S1; S2: namentlich nicht identifizierte Schüler
Ss: mehrere Schüler
L: Lehrerin
/ bzw. \: Stimme wird gehoben bzw. gesenkt
– Stimme bleibt in der Schwebe
. .. … Sprechpausen (mehr Punkte entsprechen längeren Pausen; Transkript enthält in den Sprechpassagen keine Satzzeichen.)
<: sprechen teilweise gleichzeitig
g e s p e r r t: gedehnt/langsam gesprochen
kursiv : Ausdruck, Gestik, Mimik, Handlungen etc.
fett : betont gesprochene Wörter
+: Ende des angegebenen Ausdrucks, Gestik, Mimik, Handlung, Atemholen
(Wort): eingeklammerte Wörter sind nicht zweifelsfrei verständlich
(unverständlich): gänzlich unverständliche Äußerung des fokussieren Schülers
Literatur
Brandt, B./Krummheuer, G. (1998): Zwischenbericht zum DFG-Projekt: Rekonstruktion von „Formaten kollektiven Argumentierens“ im Mathematikunterricht der Grundschule. Freie Universität Berlin, Fachbereich Erziehungswissenschaft, Psychologie und Sportwissenschaft. S. 46ff
Goos, M./Galbraith, P. u.a.( 1996): When does student talk become collaborative mathematical discussion. Technologhy in Mathematics Education: Ninteenth Annual Conference of the Mathematics Education Research Group of Australia, Melbourne, MERGA.
Nutzungsbedingungen:
Das vorliegende Dokument ist ausschließlich für den persönlichen, bzw. nicht-kommerziellen Gebrauch bestimmt – es darf nicht für öffentliche und/oder kommerzielle Zwecke außerhalb der Lehre vervielfältigt, bzw. vertrieben oder aufgeführt werden. Kopien dieses Dokuments müssen immer mit allen Urheberrechtshinweisen und Quellenangaben versehen bleiben. Mit der Nutzung des Dokuments werden keine Eigentumsrechte übertragen. Mit der Verwendung dieses Dokuments erkennen Sie die Nutzungsbedingungen an.