Fallanalysen aus demselben Erhebungskontext:

• Krummheuer, Götz: Drei Jungen bei einer Zahlenfolge

Falldarstellung

Die (…) Beispiele entstammen einem Beobachtungsmaterial zur Gruppenarbeit im Mathematikunterricht der Grundschule (genaueres s. KRUMMHEUER 1997). Entsprechende Schüleraktivitäten werden in regulären Unterrichtsstunden mit der Videokamera aufgezeichnet. Für relevant erachtete Episoden werden transkribiert und mit dem Verfahren der Interaktionsanalyse ausgewertet.

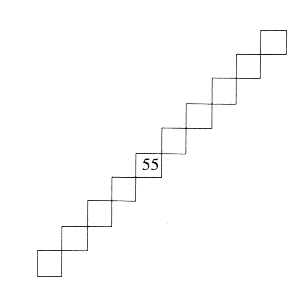
Die beiden Zweitklässler Tamara und Samanta sitzen zusammen über Aufgabenblättern zur Hundertertafel. Jeweils nur mit einer Zahl versehene Ausschnitte dieser Tafel sind vorgegeben; sie sollen die abgebildeten freien Felder ausfüllen. Die erste Aufgabe mit den Feldern in waagerechter Anordnung haben sie bereits richtig bearbeitet. Die zweite von ihnen ausgewählte Aufgabe ist die mit der diagonalen Anordnung der Felder. Bei der Bearbeitung dieser Aufgabe kommt es zu einem längeren Gespräch, von dem nur der folgende Ausschnitt wiedergegeben wird (Die erwartete Lösung besteht aus den Zahlen 91, 82, 73, 64, 55, 46, 37, 28, 19 und 10 von unten links nach oben rechts gelesen. Zu dieser Episode s. a. VOLLMER & KRUMMHEUER 1997.)

48	Tamara	Hier 55 dann fünf und – 56
49	Samanta	Dann kommt 57
50	Tamara	Genau (..) (Tamara schreibt ins 73er-Feld) was kommt dann’
51	Samanta	58
52	Tamara	Genau (schreibt) (…) und dann’
53	Samanta	60
54	Tamara	Tsesetse’ hast was ausgelassen’
55	Samanta	Äh’ S9
56	Tamara	Genau’
57		(3 sec; Tamara schreibt)
58<	Tamara	Und hier kommt dann’ (zeigt auf das 46er-Feld) (.) 54
59<	Samanta	54
60	Tamara	Ups Entschuldigung
61	Samanta	54 (Tamara schreibt)
62	Tamara	Und da’
63	Samanta	Da kommt 53.
64	Tamara	(schreibt) Genau’ bin schon mitten drin.
65	Samanta	Dann kommt 52.
66	Tamara	Genau’ geht glaub bis 50
67	Samanta	Ja (…) dann kommt 51 danach.
68	Tamara	Stimmt.
69	Samanta	Und danach kommt dann 50.
70	Tamara	Genau.
71		( 3 sec; Tamara füllt die Aufgabe fertig aus)

Die Arbeitsschritte und deren Aufteilung unter Samanta und Tamara wurden bereits in der zuvor behandelten Aufgabe entwickelt. Sie zeichneten sich durch folgende Grundstruktur aus:

• Schülerin A nennt die Zahl, die ins nächste Kästchen geschrieben werden soll und
• Schülerin B trägt diese Zahl in das entsprechende Feld ein.

Die dabei je zu bestimmende Zahl ergibt sich durch Weiterzählen bzw. Zurückzählen in Einerschritten.

Eine für den ersten Aufgabenteil erfolgreiche Strategie wenden die beiden Mädchen bei dem vorgelegten zweiten Aufgabenabschnitt erneut an. Allem Anschein nach sind Tamara und Samanta von der Richtigkeit ihrer Lösung „völlig“ überzeugt. Ergänzend erwähnt sei, dass selbst zwei später stattfindende Interventionen der Lehrerin, die die beiden Schülerinnen zu einem erneuten Überdenken der Lösung hätten veranlassen können, von ihnen in der festen Überzeugung, diesen Aufgabenteil richtig gelöst zu haben, abgetan werden.

Interpretation

Wie kommt es nun, dass sie sich so sicher sind? Wie stellen sie für sich die Rationalität ihres Lösungsansatzes klar, die dazu führt, dass sie die Aufgabe für richtig gelöst halten? Dem unterlegten theoretischen Ansatz entsprechend, wird auch bei falschen Lösungen davon ausgegangen, dass die Schüler sich bei ihren Bearbeitungsversuchen von einer gewissen Rationalität leiten lassen. Das Spezifische bei der interaktionsanalytischen Auswertung solcher gemeinsamer Bearbeitungsprozesse ist das Bemühen, in der Interaktion selbst nach Anzeichen zu suchen, die diese Rationalität zum Ausdruck bringt. Dies wird gleichsam als der argumentative Aspekt der Schülerinteraktion verstanden.

Ich erwähnte die Lösung zur ersten Aufgabe. Die den beiden Mädchen für die zweite Aufgabenlösung zu unterstellenden rationalen Anteile und Überlegungen finden u.a. ihren Ursprung in der Wiederholung dieser Weiterzählstrategie. Schüler wissen aus Erfahrung, dass Aufgabenblätter häufig mit derselben Strategie gelöst bzw. nach einem „Schema F“ abgearbeitet werden können. Auf ein solches Erfahrungswissen mögen Samanta und Tamara hier rekurrieren. Sie dürften dennoch genauso gut wissen, dass man sich nach der erfolgreichen Lösung einer Aufgabe nicht völlig sicher sein kann, bereits die für alle Aufgaben zulässige Lösungsstrategie gefunden zu haben. Ebenso dürften sie die Erfahrung gemacht haben, dass es auch vorkommen kann, dass nicht für alle Aufgaben eines Blatts dasselbe Schema F angewendet werden kann.

Die beiden Schülerinnen müssen sich deshalb absichern oder vergewissern, dass es bei dieser zweiten Aufgabe genauso geht, wie bei der ersten. Aus dem Transkript kann man kaum aufkommenden Zweifel an ihrer Vorgehensweise identifizieren. Wie machen sie sich gleichsam gegenseitig sicher? Zum ersten gilt es hierbei zu bedenken, dass es im ersten Schuljahr eine Vielzahl ähnlicher Aufgaben gibt, bei denen die Kinder in Zahlenschlangen, gewundenen Messbändern u. a. Zahlen in der kanonischen Reihenfolge der natürlichen Zahlen eingeben sollen. Zum zweiten kann man vermuten, dass für Tamara und Samanta vom Zahlenraum bis 100 noch eine gewisse Faszination des Neuen ausgeht und sich somit in dem Weiterzählen auch ein gewisses Erfolgsgefühl ausdrückt.

In dem Aufzählen von Teilstücken der Zahlreihe durch Grundschul- und Vorschulkinder wird zum dritten eine narrative Struktur an sich gesehen: Sie ist hoch sequentiell, und ihr Erwerb ist verwoben mit dem allgemeinen Spracherwerb, der seinerseits narrativ geprägt ist. Das Zählen hat für diese Kinder (noch) den Charakter des Er-Zählens. Mit der Auf-Zählung einer solchen Reihung vergewissern sie sich gegenseitig der Richtigkeit der Zahlreihe. Das Vor-Zählen stellt so etwas wie eine nicht weiter bezweifelbare Grundüberzeugung dar. Unabhängig von den Intentionen des Aufgabenstellers schaffen sich so die beiden Mädchen im interaktiven Austausch selbst Bedingungen für ihr Lernen der Zahlenreihe bis 100 (bzw. konkret bis 60). Im unterstellten Sinne des Aufgabenblattes lösen sie freilich diesen Aufgabenteil falsch.

Transkriptionsregeln

Das Transkript enthält, soweit rekonstruierbar:
– die verbalen Äußerungen der Beteiligten und
– die nonverbalen Aktivitäten, wie z. B. auffällige Körperhaltungen, auffallende Blickrichtungen, Zeichnungen auf der Tafel usw.

Linguistische Zeichen:
(a) Identifizierung des Sprechers:

L   Lehrer
S   Schüler
S 1   Kennzeichnung der Schüler, wenn eine Unterscheidung zwischen verschiedenen nicht genauer identifizierbaren Schülern nötig wird
Max   Kennzeichnung eines mit Namen identifizierten Schülers

(b) Charakterisierung der Äußerungsfolge:

Wegen der häufig im Unterricht auftretenden gleichzeitigen bzw. zeitlich nur leicht verschobenen Äußerungen wird im Bedarfsfall eine Partiturschreibweise verwendet. Die zueinander verschobenen Äußerungen geben ihre „Einsätze“ in Relation zu den anderen Äußerungen an. Das Zeichen „<“ nach der Zeilennummerierung weist auf diese Partiturleseweise hin, z. B.:

4 < L: die Fläche eines Rechteckes
5 < Sl: Uaach
6 < S2: Länge mal Breite
7 < S3: Fläche oder oder Inhalt
8 < S4: Flasche
9 < S5: Länge mal Breite
10 < S6: Ja mein ich doch

Paralinguistische Zeichen:

, kurzes Absetzen innerhalb einer Äußerung
(.) kurze Pause (max. 1 sec.)
(..) kurze Pause (max. 2 sec.)
(…) längere Pause (max. 3 sec)
(4 sec) Pause mit Angabe der Länge
. Senken der Stimme am Ende einer Äußerung
– Stimme bleibt in der Schwebe am Ende einer Äußerung
‚ Heben der Stimme am Ende einer Äußerung

Unterstreichung für auffällige Betonung
gebrochene Unterstreichung für Dehnung des Wortes

Charakterisierung der non-verbalen Aktivitäten:
Non-verbale Aktivitäten werden in die transkribierten Äußerungen eingeklammert eingefügt und durch einen anderen Schrifttyp zusätzlich gekennzeichnet.

Literaturangaben:

Krummheuer, Götz (1997): Narrativität und Lernen. Mikrosoziologische Studien zur sozialen Konstitution schulischen Lernens. Weinheim.

Vollmer, N./Krummheuer, Götz (1997): Anfangen – Machen – Helfen. Zur Beziehung zwischen Arbeitsteilung und Aufgabenverständnis während einer Partnerarbeit im Mathematikunterricht. In: Journal für Mathematikdidaktik 18 (2/3): 217-244

 Nutzungsbedingungen:
Das vorliegende Dokument ist ausschließlich für den persönlichen, bzw. nicht-kommerziellen Gebrauch bestimmt – es darf nicht für öffentliche und/oder kommerzielle Zwecke außerhalb der Lehre vervielfältigt, bzw. vertrieben oder aufgeführt werden. Kopien dieses Dokuments müssen immer mit allen Urheberrechtshinweisen und Quellenangaben versehen bleiben. Mit der Nutzung des Dokuments werden keine Eigentumsrechte übertragen. Mit der Verwendung dieses Dokuments erkennen Sie die Nutzungsbedingungen an.