- „Förderung durch materialgeleitetes Lernen im Mathematikunterricht – Der Fall Matthias“
- „Förderung durch materialgeleitetes Lernen im Mathematikunterricht – Zusammenfassende Betrachtung“
Falldarstellung mit interpretierenden Abschnitten
Saskias[1] Mathematikleistungen bescherten ihr häufig Misserfolgserlebnisse, was dazu führte, dass sie das Fach nicht mochte. Sie kam in den Förderunterricht, um alle Rechenoperationen noch einmal zu üben. Die Studentin begann, mit Saskia am Schulabakus[2] zu addieren. Aufgaben ohne Übertrag, bei denen die Plättchen auf den einzelnen Feldern zusammengeschoben und das Ergebnis abgelesen wird, bereiteten der Schülerin keine Schwierigkeiten. Als nächstes stellte die Studentin eine Aufgabe mit Übertrag (116 + 128). Saskia legte die Aufgabe mit Plättchen und fing wie gewohnt an, diese auf jedem Feld zusammenzuschieben. Die Frage nach dem Ergebnis blieb zunächst unbeantwortet. Als die Studentin nach dem Problem fragte, erklärte die Schülerin, dass es die vierzehn Plättchen auf dem Einerfeld seien.
Studentin: Woraus setzt sich vierzehn zusammen?
Schülerin: In der Zahl steckt ein Zehner.
Die Schülerin nahm nun zehn Plättchen aus dem Einerfeld und begann, sie in das Zehnerfeld zu legen. Dabei wurde sie von der Studentin unterbrochen.
Studentin: Dass du die zehn Plättchen aus dem Feld [zeigt auf das Einerfeld] wegnimmst, ist schon mal richtig. Aber kannst du die zehn Plättchen so in das Zehnerfeld legen?
Schülerin: Wenn ich sie hier wegnehme [meint die Plättchen aus dem Einerfeld] gehören sie in das nächste [meint das Zehnerfeld].
Die Studentin legte Saskia folgendes Bild und fragte sie, was sie sehe.
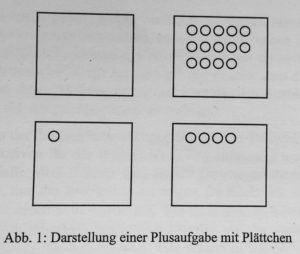
Schülerin: Es liegen oben und unten vierzehn.
Studentin: Ja. und welche Zahl hast du schneller erkannt?
Schülerin: Die untere. Oben habe ich erst gezählt
Studentin: Und wie kann das sein: die gleiche Zahl und unterschiedliche Bilder?
Schülerin: Weil hier [zeigt auf die obere Abbildung] zehn Plättchen weggenommen sind und dafür ein Plättchen [zeigt auf die untere Abbildung] in das andere Feld gelegt wurde.
Studentin: Wir müssen immer zehn Einer zu einem Zehner bündeln. Dafür wandert ein Plättchen in das nächste Feld.
Dann kehrten sie zur Aufgabe zurück und lösten sie durch Legen am Abakus. Dass der Wechsel der zehn Einerplättchen in ein Zehnerplättchen auf der symbolischen Ebene als Übertrag notiert wird, hätte an dieser Stelle dem Förderprinzip des intermodalen Transfers entsprochen.
Fußnoten:
[1] Der Name wurde geändert, um die Anonymität der Schülerin zu wahren.
[2] Als Schulabakus wurden quadratische Pappkärtchen in der Größe 12 x 12 cm und Legeplättchen zur Verfügung gestellt. Den Schüler/innen wurde erklärt, dass dem Abakus das Stellenwertsystem zugrunde liegt und in den Feldern mit Hilfe einer entsprechenden Anzahl von Plättchen die Zahlen veranschaulicht werden (Johann & Matros 2001, S. 30ff).
Literaturangabe:
Johann, Michael / Matros, Norbert (2001): Wechselspiele: kreatives Rechnen am Schulabakus. Landau: Knecht-Verlag.
Mit freundlicher Genehmigung des Schneider Verlages. http://www.paedagogik.de/index.php?m=wd&wid=1307
Nutzungsbedingungen:
Das vorliegende Dokument ist ausschließlich für den persönlichen, bzw. nicht-kommerziellen Gebrauch bestimmt – es darf nicht für öffentliche und/oder kommerzielle Zwecke außerhalb der Lehre vervielfältigt, bzw. vertrieben oder aufgeführt werden. Kopien dieses Dokuments müssen immer mit allen Urheberrechtshinweisen und Quellenangaben versehen bleiben. Mit der Nutzung des Dokuments werden keine Eigentumsrechte übertragen. Mit der Verwendung dieses Dokuments erkennen Sie die Nutzungsbedingungen an.
