Falldarstellung

Ein Beispiel (…) verdeutlicht, wie eine Argumentation erst durch non-verbale Handlungen explizit und damit rekon­struierbar bzw. nachvollziehbar wird. Benno hat seinen Auf­gabenbearbeitungsprozess einmal präsentiert und dabei ein Tafelbild entwickelt:

5 cm + 6 cm = 11cm

8 mm + 4 mm = 12mm

11 cm + 12 mm = 12 cm 2 mm

Zur Illustration wird hier zunächst eine verkürzte Darstel­lung, welche die non-verbalen Verweise vernachlässigt, ange­boten.

Transkript 1: „Die hab isch hier raus“, <413-446>, Vernachlässigung non-verbaler Komponenten

Fokussiert seien insbesondere die Zeilen 429-438. Ohne einen Anhaltspunkt, von welchen Zahlen bzw. Ziffern Benno hier spricht, bliebe das Spektrum möglicher Lesarten so groß, dass eine Rekonstruktion seiner Argumentation sehr schwie­rig würde. Erst die non-verbalen Verweise auf bestimmte Stel­len, Ziffern und Maßzahlen an der Tafel lässt Bennos Erklä­rung zu einer für Rezipienten nachvollziehbaren und über­zeugenden Argumentation werden.

Ein Rückgriff auf obiges Beispiel „Isch hatt auch so“ illu­striert zusätzlich zwei weitere Varianten, wie die Explizität der Argumentation durch die grafischen Elemente ‚Schüler­werke‘ und ‚Tafel‘ verbessert werden kann.

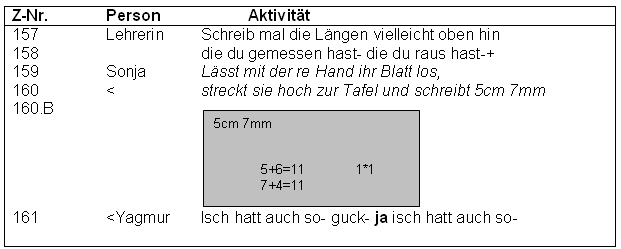
Transkript 2: „Isch hatt auch so“

Interpretation

Zum einen bietet die Tafel die Möglichkeit, einzelne Elemente der Argumentation zu veröffentlichen. Im gegebenen Beispiel (Transkript 2) fordert die Lehrerin Sonja auf, ihre Längenangaben „oben hinzuschreiben“. Dadurch werden diese Angaben zunächst der Diskussion zugänglich. Jeder hat die Möglichkeit Einwände vorzubringen. Sobald Einigung im Klassenplenum erzielt ist, sind die 5 cm 7 mm als Datum zu verstehen, welches ‘schwarz auf weiß‘ zu lesen ist. Das Gegebene ist explizit gemacht worden. Darauf lässt sich Bezug nehmen, es kann einen ‘weiteren Verlauf‘ des Argu­mentationsprozesses geben.

Zum anderen zeigt dieses Beispiel die Möglichkeit auf, dass einzelne Kinder jederzeit während der Veröffentlichungs­phase zwischen ihrem eigenen Werk und dem Tafelanschrieb vergleichen können. Dabei können sie entweder Konsisten­zen identifizieren, oder aber Unstimmigkeiten feststellen (Fetzer 2006a; b). In Transkript 2 wird die Identifikation der Übereinstimmung des Datums 5 cm 7 mm für Yagmur zum Auslöser, sich aktiv in das Interaktionsgeschehen einzubrin­gen. Die Möglichkeit, beide grafischen Elemente zu verglei­chen, gibt insbesondere dann die nötige Sicherheit sich zu Wort zu melden, wenn Inkonsistenzen bestehen. Wenn den Grundschülerinnen und Grundschülern die Unstimmigkeiten gleichsam ‘ins Auge springen‘, nehmen sie sich leichter ein Herz und bringen dies zur Sprache. Denn „Hä? … Ja aber . . . Verstehe ich nicht“ sind für Schülerinnen und Schüler grund­sätzlich ‘risikoreichere‘ Beiträge im Mathematikunterricht der Grundschule als Äußerungen der Form „Ja, habe ich auch so.“ Auf der Basis des Vergleichs zwischen eigenem Werk und Tafelanschrieb greifen Schülerinnen und Schüler jedoch ver­mehrt und gezielt in den Argumentationsprozess ein (vgl. Fet­zer 2006a; b; 2005). Dabei beziehen sich die Beiträge zum Argumentationsprozess durchaus nicht ausschließlich auf das Datum. Auch Nachfragen nach dem Garanten oder Bezug­nahmen auf die Konklusion sind immer wieder zu beobach­ten.

Wie begründen und erklären Grundschüler und Grund­schülerinnen? Im Mathematikunterricht der Grundschule wird von den Kindern vor allem substanziell argumentiert. Dabei ist es insbesondere die Unsicherheit auf argumenta­tionstheoretischer Ebene des substanziellen Schlusses, die den nötigen Raum für eine Fortführung des Argumentations­prozesses bietet. Die Vagheit fordert zu weiteren Argumenten heraus. Um jedoch an bereits Gesagtes anknüpfen zu können, ist ein Mindestmaß an Explizität der Argumentationen erfor­derlich. Der Einsatz der Arbeit mit Schreibanlässen kann die Explizität erhöhen, wenn man die Kinder anregt, ihre Ideen und Ansätze an der Tafel zu veröffentlichen und sie auf der Grundlage ihrer eigenen schriftlich fixierten Werke diskutie­ren lässt. Eine „lively discussion“ (Bruner 1996, S. 23), eine lebhafte Diskussion über mathematische Inhalte entsteht.

Literatur:

Bruner, Jerome (1996): The culture of education. Harvard University Press, Cambridge, MA.

Fetzer, Marei (2006a): Veröffentlichen im Mathematikunterricht-ein Beitrag zu einer Interaktionstheorie graphisch basierten Lernens. In: Jung­wirth, H. & Krummheuer, G. (Hrsg.): Der Blick nach innen: Aspekte der alltäglichen Lebenswelt Mathematikunterricht. Mün­ster, S. 53-84.

Fetzer, Marei (2006b): Empirische Studie zur Entwicklung von Elementen einer Interaktionstheorie grafisch basierten Lernens- Schreibanlässe im Mathematikunterricht der Grundschule. Dissertation.

Fetzer, Marei (2005): Wie beeinflussen schriftlich fixierte Schülerwerke den Interakrionsprozess? – Ein Analyseproblem. In: Beiträge zum Mathematikunterricht. Hildesheim.

Nutzungsbedingungen:
Das vorliegende Dokument ist ausschließlich für den persönlichen, bzw. nicht-kommerziellen Gebrauch bestimmt – es darf nicht für öffentliche und/oder kommerzielle Zwecke außerhalb der Lehre vervielfältigt, bzw. vertrieben oder aufgeführt werden. Kopien dieses Dokuments müssen immer mit allen Urheberrechtshinweisen und Quellenangaben versehen bleiben. Mit der Nutzung des Dokuments werden keine Eigentumsrechte übertragen. Mit der Verwendung dieses Dokuments erkennen Sie die Nutzungsbedingungen an.