• Interaktionsprozesse beim Gruppenpuzzle im Mathematikunterricht – Vortragvorbereitung in der Expertengruppe
• Interaktionsprozesse beim Gruppenpuzzle im Mathematikunterricht – Neles Vortrag in ihrer Stammgruppe
• Interaktionsprozesse beim Gruppenpuzzle im Mathematikunterricht – Vergleichende Zusammenfassung der drei Szenen

Falldarstellung mit interpretierenden Abschnitten

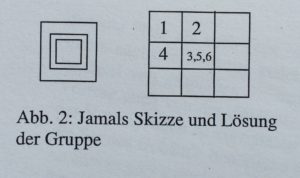
In der ersten Arbeitsphase geht es um die kollektive Lösungsfindung in den Exper­tengruppen; in der beobachteten Gruppe sind alle vier Kinder aktiv-produktiv betei­ligt. Als Ausgangspunkt für die Gruppenarbeit baut Nele das abgebildete Gebäude auf dem noch leeren Bauplan und umfährt es mit dem Stift. Sie setzt damit den Lösungshinweis in konkrete Handlung um und formuliert schließlich die Frage: ja und wie wir des hochbaun müssten/ [Stimme wird leiser] wüsste ich auch nicht/. Sie fokussiert damit das auch durch den Tipp nicht gelöste Problem, die dritte Dimensi­on (hochbaun) auf der zweidimensionalen Vorlage festzuhalten. Alle anderen Kin­der der Gruppe sind von ihr gleichermaßen als Gesprächspartner adressiert und könnten den nächsten Turn ergreifen. In den nächsten zwei Minuten werden in der Gruppe drei verschiedene Möglichkeiten zur Darstellung der dritten Dimension gefunden. [1]Die gesamte Szene lässt sich im Anschluss an diese „themeninitiierende Äußerung“ (Goffman 2005, S. 213) als eine Verkettung interaktionaler Verdichtun­gen beschreiben, die auf das Problem Hochbauen fokussieren und damit die von Nele an alle als Gesprächspartner gerichtete Frage abarbeiten. Zunächst zeigt Jamal auf, wendet sich mit ich weiß es an Nele und folgt ihrer Aufforderung (wie/), den Vorschlag zu erklären, zunächst verbal. Später zeichnet er auf das vor ihm liegende Blatt für den Turm konzentrische Quadrate, mit Höhenlinien vergleichbar (s. Abb. 2.). Allerdings fühlt sich Charline nicht verpflichtet, seinem Vorschlag ebenfalls als Gesprächspartnerin aufmerksam zu folgen, sondern ist vielmehr bemüht, mit wie­derholten guck und Bauaktivitäten auf dem Bauplan, der direkt vor Nele liegt, deren Aufmerksamkeit als Gesprächspartnerin zu gewinnen, was ihr schließlich auch ge­lingt. Ihre Lösung lässt sich als Versuch interpretieren, Grundriss und Aufriss des Gebäudes aufzuzeichnen. Diese Lösung wäre weiter ausdifferenziert unter mathema­tischen Aspekten durchaus richtig, ist aber nicht mit dem Hinweis

Dieser Platz reicht aus. (s.o.) vereinbar; Nele kommentiert den Vorschlag entsprechend: ja- aber dafür haben wir nicht genug Platz/. Sowohl von Jamal als auch von Charline wird somit Nele, bezogen auf ihre Ausgangsfrage, als Gesprächspartnerin für mögliche Lösungen angesprochen, während die anderen Kinder nur als Zuhörer beteiligt sind bzw. sich als Zuhörer angesprochen fühlen und somit keine Verpflichtung zur Stellungnahme empfinden. Diese Interpretation wird auch dadurch bestärkt, dass Jamal seinen Blick schließlich auf die Aushandlung zwischen Charline und Nele richtet und an einer ihm geeigne­ten Stelle Nele seine fertige Zeichnung präsentiert (also so). Allerdings nutzt Jens fast zeitgleich die Gelegenheit, ihr seine Lösung anzubieten (oder wir zei das ginge auch/ wenn wir/). Er macht zwar deutlich, dass er die anderen Vorschläge akustisch wahrgenommen hat, bindet seinen Beitrag aber argumentativ nicht an die von Jamal und Charline präsentierten Vorschläge an. Vielmehr scheint er diese beiden Lö­sungsvorschläge thematisch zu übergehen und nun als Sprechender direkt auf Neles Ausgangsfrage zu reagieren – dies entspricht dem Zuhörerstatus für die vorherge­henden Antworten auf die Initiationsfrage. [2] Dass auch er sich an Nele als Ge­sprächspartnerin wendet, während den beiden anderen zunächst der Zuhörerstatus zugewiesen wird, lässt sich beispielsweise an folgender Sequenz ablesen, in der er, ungeachtet der kurzen Aushandlung zwischen Charline und Jamal, seinen eigenen Lösungsvorschlag weiter vorträgt:

Charline reagiert hier nicht auf Jens Beitrag sondern auf Jamals Zeichnung und adressiert dafür Jamal explizit als Gesprächspartner; ihrer Situationsdefinition zufol­ge ist sie berechtigt, ein „Byplay“ (Brandt 1998, S. 315) zwischen Zuhörern aufzu­bauen und sie wird darin durch die Reaktionen der anderen bestärkt. Gleichwohl reagiert sie kurz danach als erste bestätigend auf die von Jens skizzierte Lösungsidee, die seine Gesprächspartnerin Nele hingegen nicht verstanden hat: das habe ich irgendwie nicht gerafft. Dieser unspezifischen Frage nachgehend klären Charline und Nele in einer wechselseitigen, dyadisch orientierten Gesprächpartnerschaft, wie Jens Lösungsidee zu verstehen sei; Jens ist dabei lediglich als Zuhörer eingebunden (und dann meint er so/ ). Am Ende ergreifen Jens und Jamal jedoch den Turn und klären, in welches Feld die Ziffern 5 und 6 einzutragen seien (Abb. 2). Damit wird die Lösung insgesamt als Gruppenlösung akzeptiert und die Grenze zur Zuhörer­schaft der anderen Kinder hin zur allgemeinen Gesprächspartnerschaft innerhalb der Gruppe wieder aufgelöst. Nach einer weiteren kurzen Klärungssequenz, die insbe­sondere zwischen Nele und Jamal ausgehandelt wird, verkündet schließlich Jens: wir ham wir hams rausgefunden\ Erstmals sind mit diesem Sprechakt Personen außerhalb der Arbeitsgruppe als Gesprächspartner angesprochen, vornehmlich wohl die Lehrpersonen. Der erste interne Lösungsprozess wird damit auch nach außen sieht- bzw. hörbar abgeschlossen.

Fußnoten

[1] Keine der Möglichkeiten entspricht der durch den Lösungshinweis anvisierten Ziellösung, was einer¬seits ein Kennzeichen für eine echte Problemaufgabe ist und andererseits von einer hohen Kreativität der Kinder zeugt.

[2] Ein ähnliches Rezeptionsmuster lässt sich im lehrerzentrierten Klassengespräch finden: Hier können im interaktionalen Gleichfluss Beiträge anderer Lernender für die thematische Anbindung übergangen werden, wenn im eigenen Redebeitrag die ursprüngliche Initiationsfrage der Lehrperson beachtet wird.

Literaturangaben

Goffman, Erving (2005): Rede-Weisen. Hrsg. von Knoblauch, Hubert u.a. Konstanz: UVK Verlagsgesellschaft.

Brandt, Birgit (1998): Recipients in Elementary Mathematics Classroom Interaction. In: Schwank, Inge (Hrsg.): Proceedings of CERME 1. Osnabrück, 27.-30.8.1998, Universität Osnabrück, URL: fmd.uni-osnabrueck.de/ebooks/erme/cermel-proceedings.html.

Nutzungsbedingungen:
Das vorliegende Dokument ist ausschließlich für den persönlichen, bzw. nicht-kommerziellen Gebrauch bestimmt – es darf nicht für öffentliche und/oder kommerzielle Zwecke außerhalb der Lehre vervielfältigt, bzw. vertrieben oder aufgeführt werden. Kopien dieses Dokuments müssen immer mit allen Urheberrechtshinweisen und Quellenangaben versehen bleiben. Mit der Nutzung des Dokuments werden keine Eigentumsrechte übertragen. Mit der Verwendung dieses Dokuments erkennen Sie die Nutzungsbedingungen an.